解读模拟合成器『10』--加法合成（下）

上一回我们说到，加法合成出的音色比较单一，那么还有什么方法去丰富他呢？既然加法合成可以生成类似于锯齿波的波形，那么为什么不把加法合成出的声音再使用减法合成的方法修饰一新呢？这确实是一个办法。

我们可以像图示10（Figure10）那样将VCF、VCA和包络发生器加入到加法合成器中，通过滤波等手段修饰音色。而更为合理的加法合成器构造应该像图示11（Figure11）那样，每个震荡器发出的波形都连接一个包络发生器控制输出，最后再混合在一起。

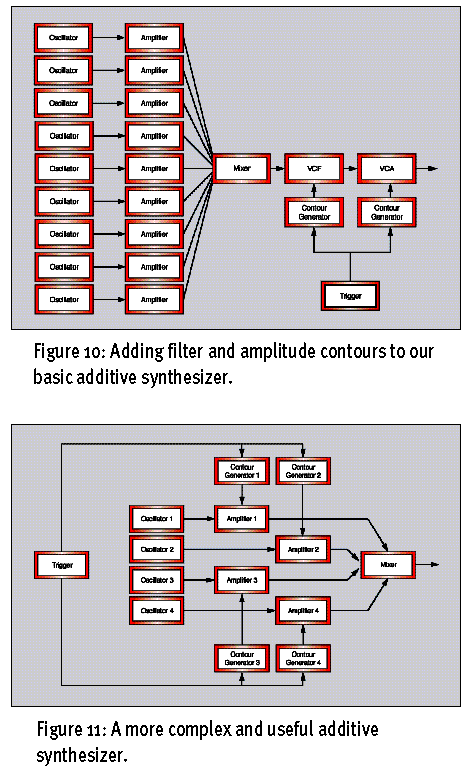
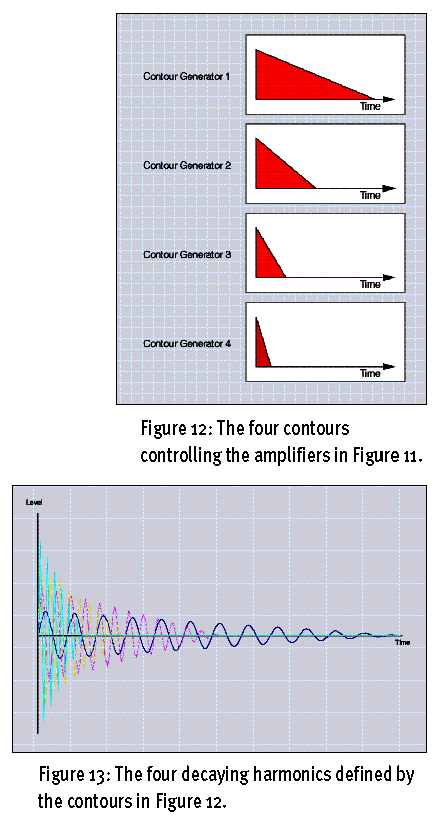
其中的震荡器1发出正弦波作为基波（也就是1次谐波），震荡器2发出正弦波作为2次谐波，后面依次类推。假设与震荡器1连接的放大器1，其声音衰减到静音的时间为T，那么与震荡器2连接的放大器2，其声音衰减到静音的时间就为T/2，以下同样依次类推。这种震荡器与放大器的关系使得低频谐波持续时间比较长，而频率越高的谐波持续的时间就越短，造成声音在刚发出时非常明亮，而随着时间的推移变得越来越暗淡（这可能有点像低通滤波器），其示意图如图示12（Figure12），4个不同的包络控制着4个拥有不同的谐波。

使用以上方法制作出来的波形会是图示13（Figure13）那样，4个不同颜色代表4个不同谐波产生的波形。图示14（Figure14）则表示出4个信号混合输出后的波形。

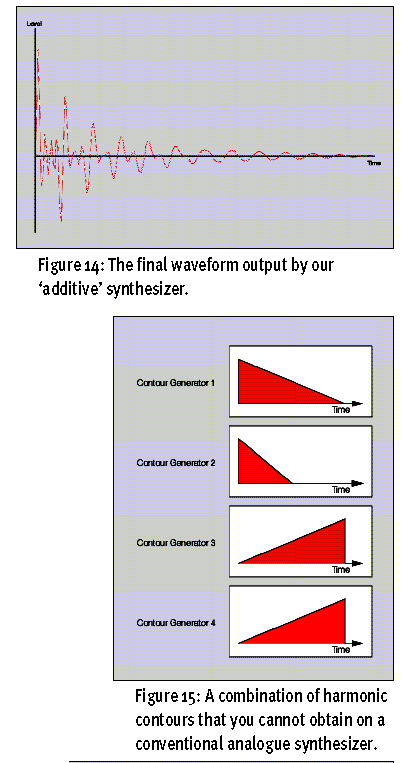
其实图示14（Figure14）的声音使用一个震荡器+一个滤波器就可以做的到，那我们干吗花大力做加法合成呢？把图示12（Figure12）中4个加法合成的包络稍做修改，就可以得到其他方法不易得到的波形。比如我们保留图示12（Figure12）中所有波形不变，前两个震荡器的包络也不变，只改变后两个震荡器的包络，使他们的声音从渐渐变小改为渐渐变大，如图示15（Figure15）。这样输出的波形会是图示16（Figure16）的样子。

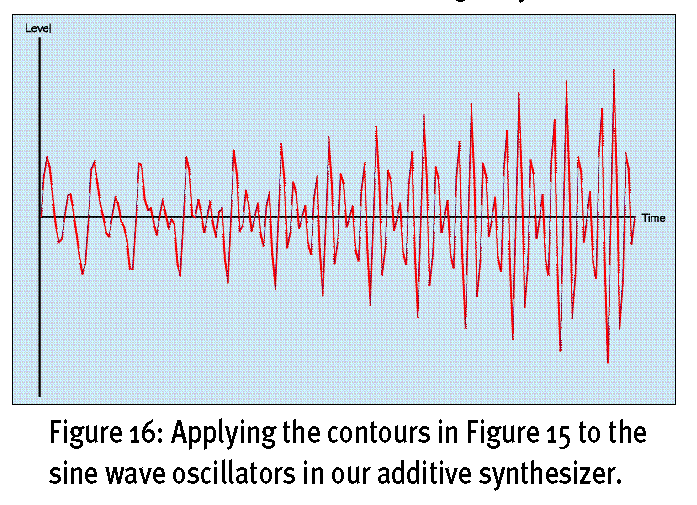
图示16（Figure16）的波形显然的与图示14（Figure14）不同了，他随着时间越来越复杂，而且高频成分占据了音符一半的部分，这种声音你是无法在Minimoog、Odyssey、Prophet 5，或者任何的单信号通路合成器中得到的，虽然Prophet 10等一些多信号通路合成器近似的得到这种声音，但是都不如加法合成器来的爽快，加法合成器允许你独立设置32次、64次、128次甚至是256次谐波的振幅。

傅里叶合成（Fourier synthesis）：

要制作更为复杂的声音，就要用到傅里叶合成（Joseph Fourier，法国数学家，他的理论现在被称为傅里叶分析，他证明了任何的声音都可以分解成无数多个正弦波），而我们这里所说的傅里叶合成就是要将这无数多的正弦波再组合成复杂的声音，当然了加法合成器的震荡器还可以发出更多的波形，不仅限于正弦波（虽然使用傅里叶合成理论正弦波就已经足够了），你还可以使用方波、锯齿波，或者更为复杂的经过脉冲宽度调制的脉冲波，这些波形还是可以被分解成正弦波，所以实际上你还是在使用正弦波来做加法合成。

要想用加法合成的方法制作一个比较复杂的音色，那么你需要超级多的震荡器发出超级多的正弦波，这在模拟合成器上很难实现，需要成千上万吨的震荡器、包络发生器、放大器和混音器。这还不算完，每个震荡器还需要相应的模块调节音高，还需要LFO增加变化，这些玩意足够占用你的整个卧室了，当你使用他们制作音乐的时候，你在哪里睡呢？所以现在的加法合成更多的出现在数字合成器中，在数字合成器中震荡器、放大器之类的模块不过是一堆等式，想要多少就有多少。

（题外话：也许你非常想知道傅里叶合成的原理，或者非常想知道使用傅里叶合成声音的原理，很遗憾这涉及到太多的纯数学知识，如果你立志想去探索的话，可以去查阅有关傅里叶合成/分析方法的数学书籍。傅里叶分析仪可以分析出声音的成分，在看到声音成分后再用加法合成的方法制作声音，是不错的选择。）

噪音惹事：

当你掌握了加法合成的方法并试图开始合成声音的时候，你并不会非常成功，因为我们上面讲的有很多都是错误地。错就错在噪音上了。

如果使用傅里叶分析长笛或小号等乐器的频谱，并将所有声音都拆成了不同的正弦波，你会发现把这些正弦波去掉之后，留下的是一片噪音，虽然声音不大，但是没有这些噪音，合成出的声音就不会很真实。所以加法合成器都需要一个噪音发生器模块，可以发出粉红噪音和白色噪音，你需要将噪音做滤波后再混入合成出的声音。

这样组合出来的合成器如图示17（Figure17），如果你事先用傅里叶分析，得到声音包含的正弦波，那么可以称为“频谱分析合成器”，如果你不分析完全凭感觉做加法合成，那么可以叫做“正弦波加噪音合成器”，哈哈玩笑了。

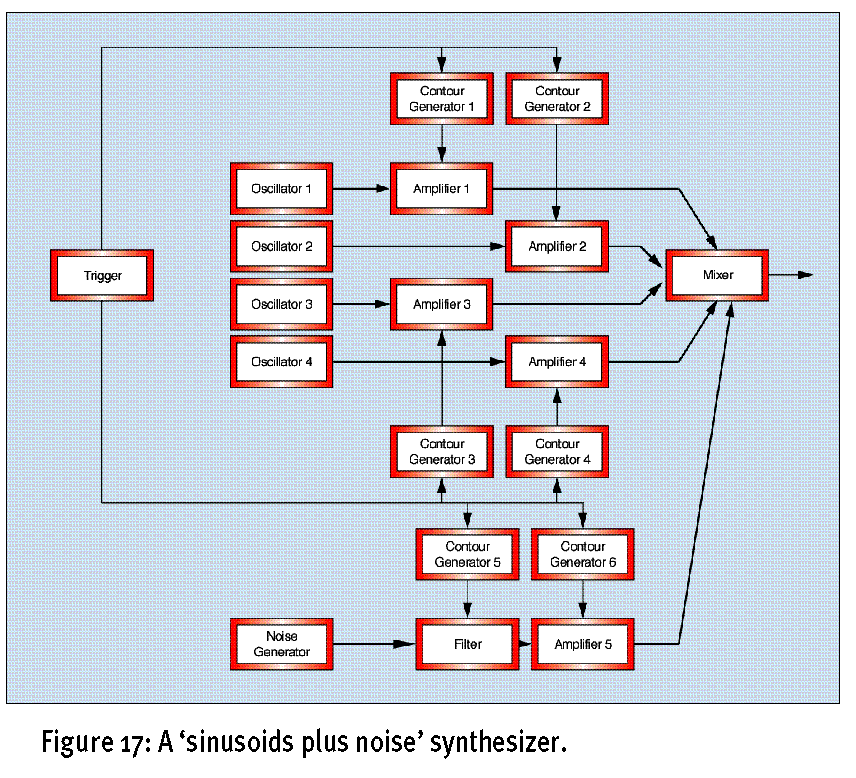
不论如何，加法合成是现在最流行的合成方法，其使用正弦波加噪音的合成方式也很有意思，一旦你身陷其中你将体会到加法合成的乐趣。

本文根据《Sound on Sound》杂志的《Synth secrets PART 14：An Introduction to Additive Synthesis》编译

midifan.com